The internet has grown to connect a very large user base in recent times, but still bandwidth remains limited. Images take up a large amount of bandwidth. Hence we make use of different image compression methods. One famous format is the JPEG(joint photographic Experts Group).This format makes use of Discrete cosine transforms. In this post we will try to understand the simple idea behind DCT(Discrete Cosine Transformations).
For our demo I will be using Octave(it is an equivalent of Matlab).
I will be using the following image, which is a 512x512 image. As shown:
For our demo I will be using Octave(it is an equivalent of Matlab).
I will be using the following image, which is a 512x512 image. As shown:
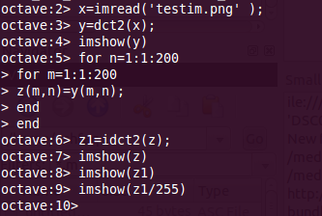
The code for understanding DCT is fairly simple.
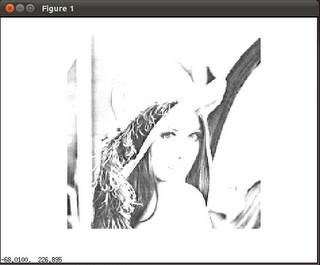
The resulting image is shown along side. Now to understand what we actually did we have to look at the details of the image.
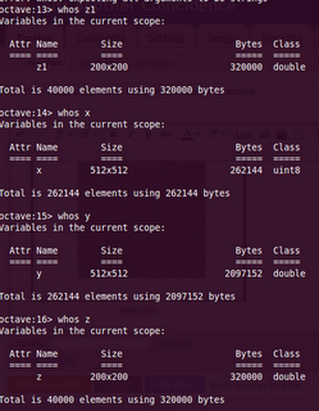
Just type in "whos z1" (without quotes)in your main terminal and u will see that the resulting image is a 200x200. Not only has the image been re-sized but the important point is we recovered the complete image with only 200x200 values of the DCT. This is what we mean by energy compaction,where the most of the image data is stored in the first few elements of the matrix. So instead of having a 512x512 information where each pixel data is important to define the picture, we have converted that to a set of 200x200 matrix where the first few entries talk about the contrast of the whole picture and the rest are data which can be 'mutiplied' in a sense of saying to the contrast to get the whole picture.
- The first line reads the image into the matrix 'x'. By this, the image can now be imagined as a matrix of 512 rows and 512 columns and each value of the matrix corresponds to the contrast of that part in the figure.for example the eyes in the image may correspond to the location of [260,256]. Therefore the matrix value at this address is 0 indicating completely black. (on a scale of 255, where 255 is white). If the picture was a colour image, the matrix would be of the size 512X3,512X3 where the first three values refer to the RGB of the first pixel(Red Blue and Green values. This is referred to as a 3 channel image).
- Next we find the DCT of this image and store it on 'y'.Remember that the DCT is not really a one to one mapping like the case above (each matrix entry is not really referring to the complete information of the picture).Instead the entries refer to the weights of the pixels. Not going much into the thoery, lets move on.
- The next 5 lines of code is used to take a part of the matrix 'y' and save it onto matrix z. Here only 200x200 elements of the matrix 'y' are saved on 'z'.The plot of 'y' and 'z' are show later.
- The above operation is similar to cropping of the image.
- Now we find the inverse DCT of the matrix 'z' this should give us the image back, but it will not. a scaling factor of around 255 is required,either multiply or divide play around to find the correct one.Divide works for me.
- Hence the line: imshow(z1/255).
The resulting image is shown along side. Now to understand what we actually did we have to look at the details of the image.
Just type in "whos z1" (without quotes)in your main terminal and u will see that the resulting image is a 200x200. Not only has the image been re-sized but the important point is we recovered the complete image with only 200x200 values of the DCT. This is what we mean by energy compaction,where the most of the image data is stored in the first few elements of the matrix. So instead of having a 512x512 information where each pixel data is important to define the picture, we have converted that to a set of 200x200 matrix where the first few entries talk about the contrast of the whole picture and the rest are data which can be 'mutiplied' in a sense of saying to the contrast to get the whole picture.


 RSS Feed
RSS Feed